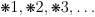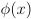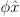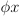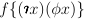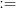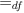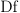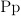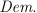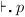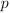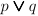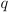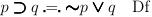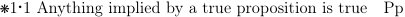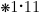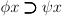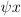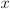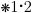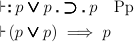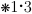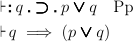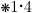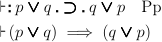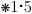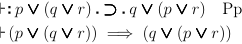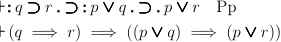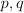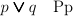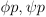Blogicisim #0 Principia *1
27 Nov 2024 -
$\require{amsmath}$
$\require{amssymb}$
$\require{amsfonts}$
Last updated 1/28/25
Intro
My main goal in writing this series of posts is to leave myself an
organized record of my thoughts to refer to later. I am posting them
online since what I write may be useful to others. Principia has a
reputation for being somewhat impenetrable, so I hope to de-mystify it
somewhat with these notes.
My aim at first will be to show the most important results in
principia’s notation, what I understand to be modern notation, and in
english. Maybe I’ll discuss some proofs but probably not…
These notes will not be based soley on the Principia itself.
According to my teacher Gregory Landini at the University of Iowa, the
Principia cannot be understood in isolation. Russell was his own worst
enemy when writing the text; some of his efforts have made the work more
obscure than it needed to be. For example, the Principia suppresses
notation that would indicate the type of propositions. To paraphrase
Landini, the entire introduction of the Principia should be skipped as
it is misleading. One should skip directly to the first chapter,  . In order to
understand Principia, we must go through the proofs and consult
secondary literature written by authors who have done the same and
understood Russell’s intentions correctly. When preparing these notes,
my references have included the following.
. In order to
understand Principia, we must go through the proofs and consult
secondary literature written by authors who have done the same and
understood Russell’s intentions correctly. When preparing these notes,
my references have included the following.
- The Basic Laws of Arithmetic by Gottlob Frege
- Principles of Mathematics by Bertrand Russell
- Introduction to Mathematical Philosophy by Bertrand Russell
- Logic and Knowledge by Bertrand Russell
- The Foundations of Mathematics by F. P. Ramsey
- Russell’s Metaphysical Logic by Bernard Linsky
- Russell by Gregory Landini
- Nice discussions of Principia, chapter by chapter, on YouTube by The
Second Number-Class
Some Core Ideas and
Motivations
On Frege
- One of Russell’s motivations was to follow up on Gottlob Frege’s
failed system, which he felled by showing that Basic Law Five causes a
paradox.
On Math
- When pure mathematicians are “doing math” they are studying
relational structures
- Math is the study of relations
On Numbers
- We should avoid making metaphysical commitments to the existence of
abstract objects like numbers
- Numbers cannot be defined using counting because counting uses
numbers
- A number is not identical to a collection of things with that number
of things in it
- Peano’s axiomatization of the natural numbers can be simplified
On Classes (and Sets)
- We should avoid making metaphysical commitments to the existence of
abstract objects like classes
- Math can make use of the idea of classes without assuming that such
things as classes actually exist
Things You May Find Weird
A contributing factor to the impenetrability of Principia by modern
readers is that Whitehead and Russell’s notation differs significantly
from what is used in contemporary presentations of logic. Speaking for
myself, I will say there is not much overlap between the notation
Whitehead and Russell use for their propositional logic and what I
learned in my introductory logic coursework in engineering and computer
science. Even the book itself has a non-standard layout.
- Principia is Unfinished - There are three published
volumes of Principia and two editions. There was supposed to be a fourth
volume (it is even referenced in volume III).
- Chapter Structure - Instead of Chapter 1, 2, 3,…,
Principia has
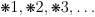 . (Sub)Sections of
the chapters are ordered by decimal places.
. (Sub)Sections of
the chapters are ordered by decimal places.
- Function Notation - Usually we would read
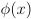 as a function. In
Principia, we would write
as a function. In
Principia, we would write 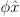 to designate the function itself and write
to designate the function itself and write
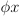 to designate an
ambiguous value of the function. These notational conventions are not
used consistently in the text. Sometimes, you will see function
expressions such as
to designate an
ambiguous value of the function. These notational conventions are not
used consistently in the text. Sometimes, you will see function
expressions such as 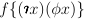 where the “argument” is not
actually an argument because it doesn’t actually exist.
where the “argument” is not
actually an argument because it doesn’t actually exist.
- Delimiters - Instead of parentheses and brackets,
you fill find dots. Numbers of dots correspond to levels of scope. Among
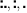 ,
,  is the broader scope and
is the broader scope and  is the narrowest
scope.
is the narrowest
scope.
- Definitions - Rather than use
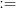 or
or 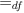 , a definition will
be followed by
, a definition will
be followed by 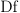 . Similarly, a
primitive will be followed by
. Similarly, a
primitive will be followed by 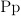
- Proofs - Rather than begin a proof with
Proof., Principia begins them with Demonstrations
signified by
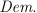
- Law of the Excluded Middle - Principia accepts the
law of excluded middle, which states that a proposition is either true
or false. You might say this is unreasonable because they hold that
future events which are uncertain such as “In 50 years I will have a
beard.”
- Truth Values - True and False are not objects in
the Principia. Truth values are used informally.
 - Primitive
Ideas and Propositions
- Primitive
Ideas and Propositions
Summary and Highlights
Principia begins by characterizing a basic propositional logic which,
other than the symbols used, is similar to what one would encounter in a
basic logic course. This logic is supported by primitive ideas and
propositions that are not (fully) defined. The reason for this is that a
system employing definitions must either be circular or be founded upon
undefined terms. Circularity trivializes a system, so the latter is
preferable.
Later, in 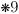 , the
propositions from here up to
, the
propositions from here up to 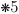 will be generalized such that any proposition
can be replaced by one with any number of quantifiers. In this way,
quantification logic will be built.
will be generalized such that any proposition
can be replaced by one with any number of quantifiers. In this way,
quantification logic will be built.
Primitives Introduced
- Elementary Proposition - Proposition with no
variables or quantifiers
- Elementary Propositional Function - Unsaturated
statement such that, when saturated, yields an elementary
proposition
- Assertion of a Proposition - Saying that the
proposition is true, rather than simply stating it. This is expressed as
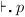 .
.
- Assertion of a propositional function - Saying that
the propositional function is true for general ambiguous argument.
- Negation -
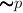 means
means 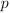 is false.
is false.
- Disjunction -
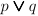 means “either
means “either 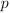 is true or
is true or 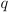 is true.”
is true.”
Implication as Material
Implication
Implication is a relation between propositions.
One proposition implying another is symbolized as 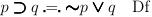 This
definition of implication is called material implication and any
feelings that this definition is odd are rightly justified. Since I am
writing this post in Iowa, the material implication “If I am in London,
then I am in France” is a true statement. There are other conventions
for characterizing implication: enthymematic, deductive, and strict.
This
definition of implication is called material implication and any
feelings that this definition is odd are rightly justified. Since I am
writing this post in Iowa, the material implication “If I am in London,
then I am in France” is a true statement. There are other conventions
for characterizing implication: enthymematic, deductive, and strict.
Primitive Propositions
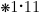 Where
Where
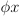 can be asserted,
can be asserted,
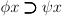 can
be asserted, then
can
be asserted, then 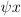 can be asserted, where
can be asserted, where 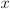 is a real variable in
each case.
is a real variable in
each case. 
We get inference rules from 1.1 and 1.11. The statement of 1.11,
although it does not include notation for type, gives some type
safety.
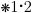 (Principle of Tautology)
(Principle of Tautology)
Any proposition implies itself.
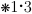 (Principle of Addition)
(Principle of Addition)
A disjunction of a true proposition with another proposition is still
true.
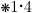 (Principle of Permutation)
(Principle of Permutation)
If a disjunction is true, the result after reversal of the terms is
still true.
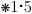 (Associative Principle)
(Associative Principle)
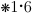 (Principle of Summation)
(Principle of Summation)
In an implication, an alternative may be added to both premiss and
conclusion without impairing the truth of the implication.
(Closure Properties)
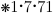
If 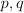 are elementary
propositions then so are
are elementary
propositions then so are 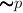 and
and 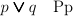
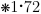 (Axiom of Identification of Real Variables)
(Axiom of Identification of Real Variables)
If 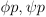 are
elementary propositional functions which take elementary propositions as
arguments, then
are
elementary propositional functions which take elementary propositions as
arguments, then  is an
elementary propositional function
is an
elementary propositional function 
 . In order to
understand Principia, we must go through the proofs and consult
secondary literature written by authors who have done the same and
understood Russell’s intentions correctly. When preparing these notes,
my references have included the following.
. In order to
understand Principia, we must go through the proofs and consult
secondary literature written by authors who have done the same and
understood Russell’s intentions correctly. When preparing these notes,
my references have included the following.